“Yeah It’s on. ”
项目介绍
![]()
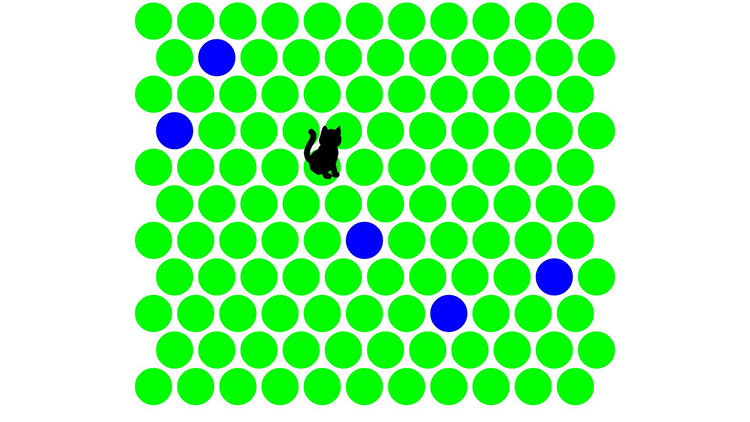
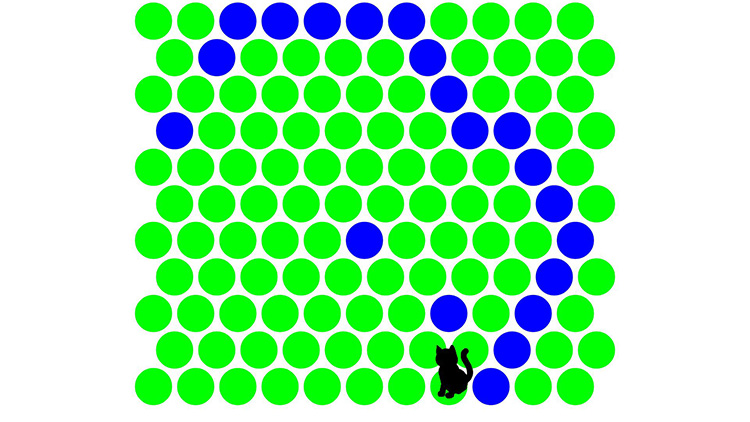
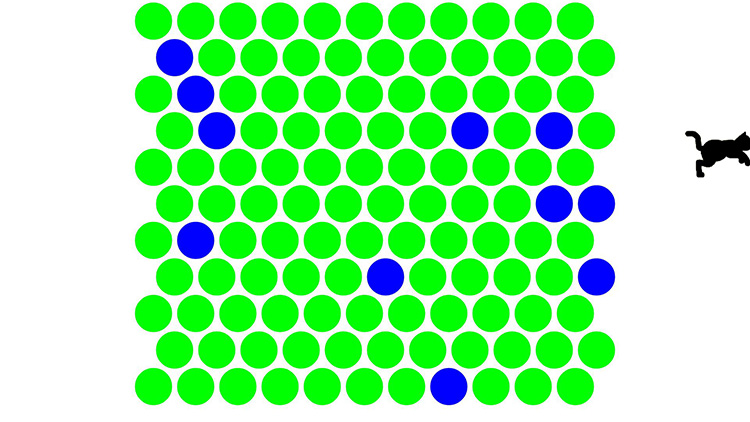
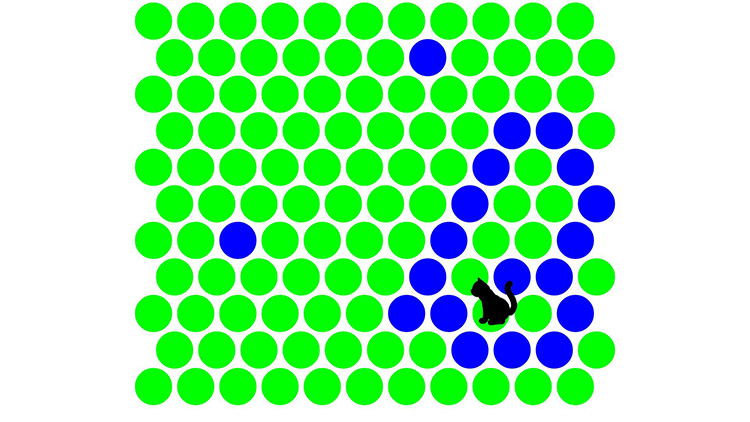
游戏目的很简单,中间有一只猫,它会想跑出屏幕,而我们能做的就是在它前面设置阻挡。也就是点下面的地板,把猫圈住就算赢了。(点一次就会多一个深色点, 目标是用深色点把猫围起来)游戏开始后,猫咪会在场景中间位置,场景中的黄绿色圈圈是可点击的,点击后变为墨绿色圈圈,墨绿色圈圈猫不能行走。用最少的步骤,把猫困起来才是高手。
也许这只猫比你想象中的更聪明,因为它懂最短路径算法。
项目源码:https://github.com/xuqiqiang/CatchCat
Dijkstra算法
定义概览
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。注意该算法要求图中不存在负权边。
问题描述:在无向图 G=(V,E) 中,假设每条边 E[i] 的长度为 w[i],找到由顶点 V0 到其余各点的最短路径。(单源最短路径)
算法描述
算法思想:
设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
算法步骤:
a.初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
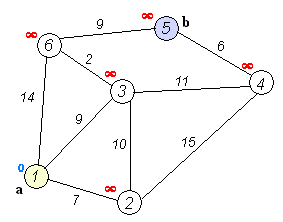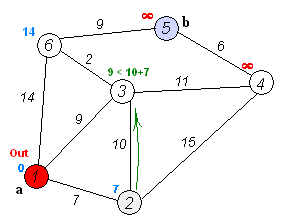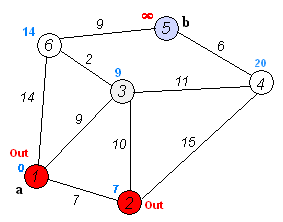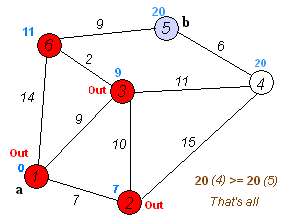
执行动画过程如下图
Dijkstra算法代码实现
const int MAXINT = 32767;
const int MAXNUM = 10;
int dist[MAXNUM];
int prev[MAXNUM];
int A[MAXUNM][MAXNUM];
void Dijkstra(int v0)
{
bool S[MAXNUM]; // 判断是否已存入该点到S集合中
int n = MAXNUM;
for(int i = 1; i <= n; ++i)
{
dist[i] = A[v0][i];
S[i] = false; // 初始都未用过该点
if(dist[i] == MAXINT)
prev[i] = -1;
else
prev[i] = v0;
}
dist[v0] = 0;
S[v0] = true;
for(int i = 2; i<=n; i++)
{
int mindist = MAXINT;
int u = v0; // 找出当前未使用的点j的dist[j]最小值
for(int j = 1; j <= n; ++j)
if((!S[j]) && dist[j] < mindist)
{
u = j; // u保存当前邻接点中距离最小的点的号码
mindist = dist[j];
}
S[u] = true;
for(int j = 1; j <= n; j++)
if((!S[j]) && A[u][j] < MAXINT)
{
if(dist[u] + A[u][j] < dist[j]) //在通过新加入的u点路径找到离v0点更短的路径
{
dist[j] = dist[u] + A[u][j]; //更新dist
prev[j] = u; //记录前驱顶点
}
}
}
}
算法实例
先给出一个无向图
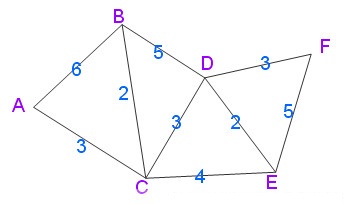
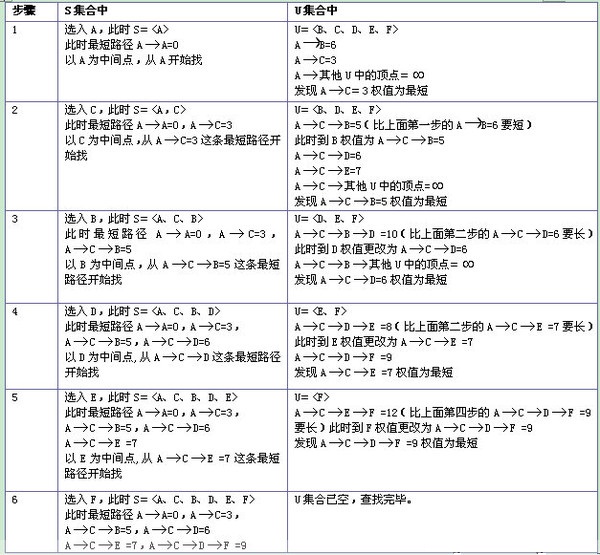
用Dijkstra算法找出以A为起点的单源最短路径步骤如下:
项目源码
https://github.com/xuqiqiang/CatchCat
截图预览


—— SnailStudio 后记于 2017.5